DeepLearning from Scratch - Ch2. Perceptron
2.1 퍼셉트론이란?
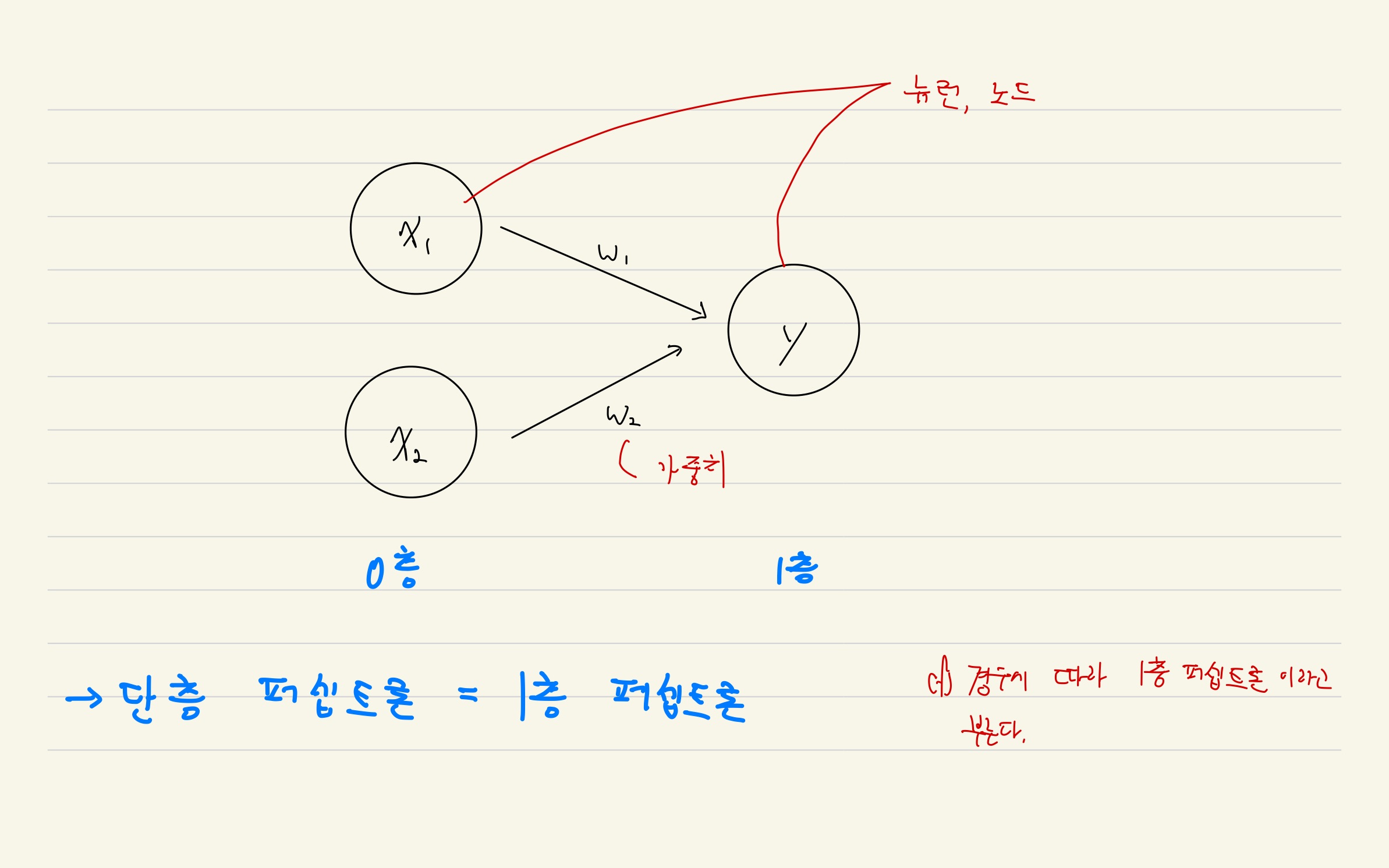
- 프랑크 로젠블라크(Frank Rosenblatt)rk 1957년에 고안한 알고리즘
- (단순) 퍼셉트론은 다수의 신호(입력)를 입력으로 받아 하나의 신호(출력)를 출력한다.
-
w, θ를 매개변수라고 한다
-
$w_1$과 $w_2$는 각 입력 신호의 결과에 대한 중요도(영향도)를 조절해준다
-
$θ$(or $b$)는 얼마나 쉽게 활성화되는지 조절해준다
-
-
뉴련에서 보내온 신호의 총합이 정해진 한계를 넘어서면 1, 넘지 못하면 0을 출력
- 이러한 한계를 임계값(threshold)라고 한다
- 1이 나오는 경우 뉴런이 활성화한다고 표현한다
-
가중치(w)가 클수록 해당 신호가 그만큼 더 중요하다는 의미이다
-
학습이란 적절한 매개변수 값을 정하는 작업이다
- 매개변수 값을 주는 것은 사람이 하는 작업이다
2.2 논리 회로와 진리표
- 입력 신호와 출력 신호의 대응 표를 진리표라고 한다.
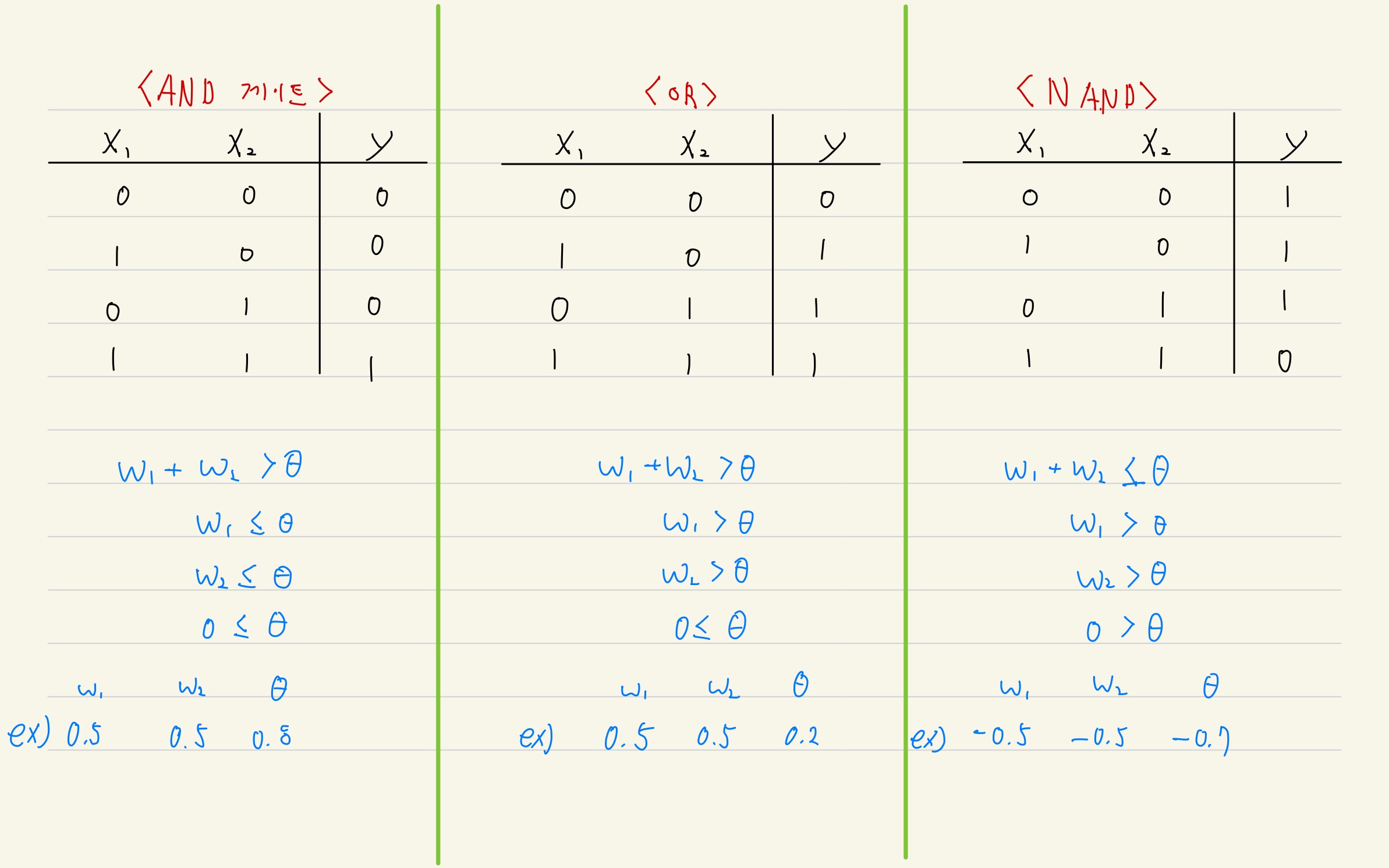
2.3 퍼셉트론 구현하기
2.3.1 AND 논리 회로 구현
def AND(x1, x2):
# 기본적인 방법으로, 개인이 직접 초기값을 설정하기
w1, w2, theta = 0.5, 0.5, 0.7
func = w1*x1 + w2*x2
if func <= theta:
return 0
else:
return 1
print(AND(1,0))
print(AND(1,1))
0
1
2.3.2 편향(Bias)
$θ$를 $-b$로 치환하고 $b$를 편향(bias)라고 하자 - 위의 식은 다음과 같이 바꿔쓸 수 있다
편향을 고려한 논리 회로
import numpy as np
x = np.array([0,1])
w = np.array([0.5, 0.5])
b = -0.7
# 브로드캐스팅에 의해 같은 위치(index)의 값끼리 곱해진다
print(w*x)
print(np.sum(w*x))
# 파이썬의 float는 부동소수점으로 연산 시 오차가 발생한다
# 이러한 문제를 해결하기 위해서는 고정소수점을 사용해야 하며 Decimal()을 사용해야 한다
print(np.sum(w*x) + b)
[0. 0.5]
0.5
-0.19999999999999996
NAND, OR 논리 회로 구현
def NAND(x1,x2):
w = np.array([-0.5, -0.5])
x = np.array([x1, x2])
# theta = -0.7 = -b
b = 0.7
func = np.sum(w*x) + b
if func <= 0:
return 0
else:
return 1
def OR(x1,x2):
w = np.array([0.5, 0.5])
x = np.array([x1, x2])
b = -0.3
func = np.sum(w*x) + b
if func <= 0:
return 0
else:
return 1
2.4 퍼셉트론의 한계
- XOR(배타적 논리합): $x_1$와 $x_2$ 중에서 한쪽이 1일때만 1을 출력하는 구조
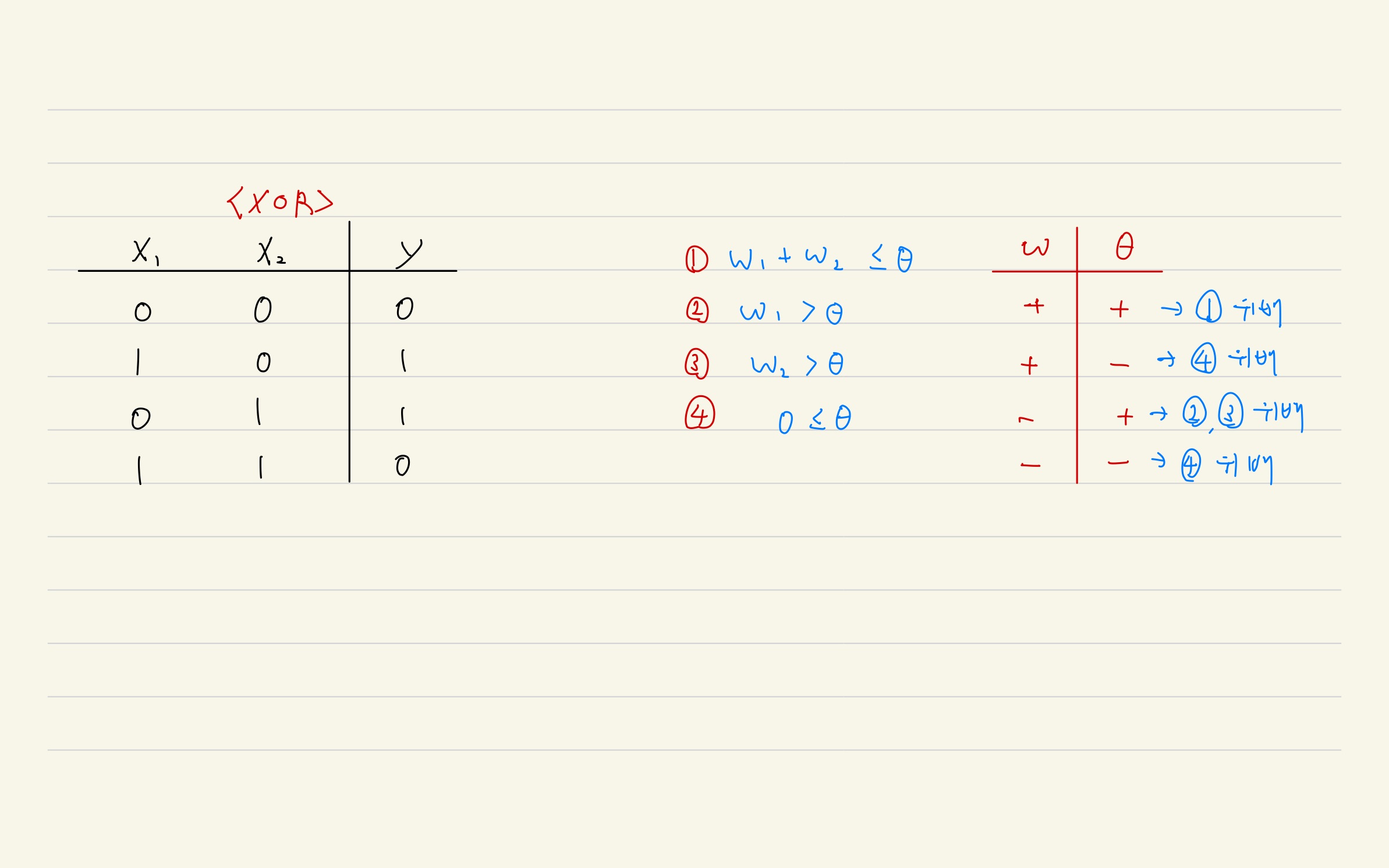

주의사항!!!
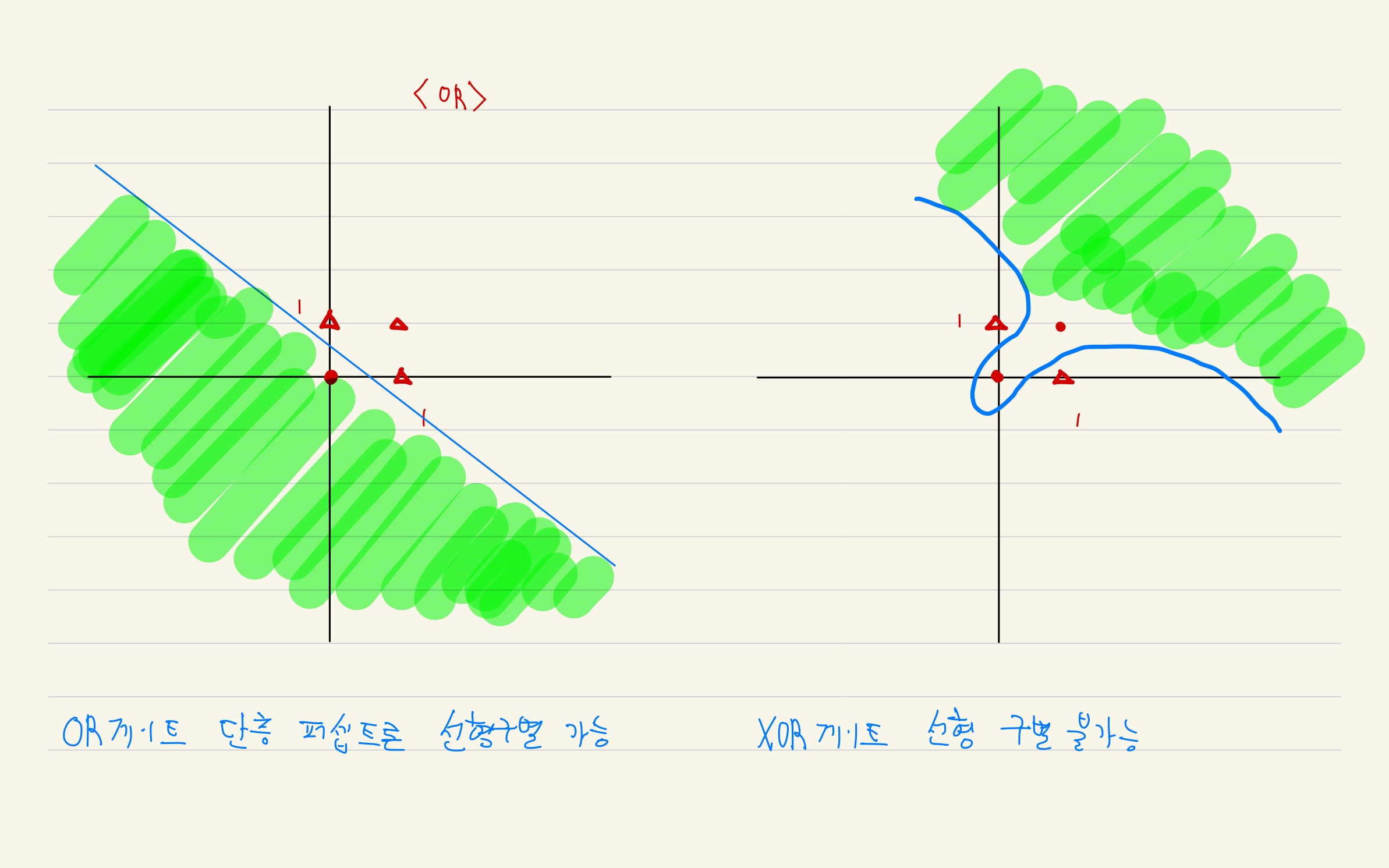
- 지금까지 설명한 퍼셉트론으로는 XOR 게이트를 구현할 수 없다
- 하나의 퍼셉트론을 쓴다는 말은 선형 모델링을 하겠다는 의미이고 이것은 XOR 문제를 풀 수 없다
- XOR 문제를 풀기 위해서는 input에 대해 NAND, OR 게이트를 구한 후, 이것의 output을 AND의 input으로 사용해야 한다
- 즉 layer(층)을 하나 더 추가해야 한다.
XOR 게이트 구현
def XOR(x1,x2):
s1 = NAND(x1,x2)
s2 = OR(x1,x2)
y = AND(s1, s2)
return y
print(XOR(0,0))
print(XOR(1,0))
print(XOR(0,1))
print(XOR(1,1))
0
1
1
0